Using breadth-first search in Shisen-Sho

Shisen-Sho (also known as Four-Rivers or simply Rivers) is a mahjong-like game, where the player needs to match similar tiles in pairs until all tiles are removed from the board.

KShisen

In this article I will cover usage of breadth-first search in implementation of Shisen-Sho game.

1. Rules

The main difference with classic mahjong solitaire games is that to remove two tiles, they must have a connection, and the connection path must not exceeed two 90° turns (in other words: the connection can have at most 3 segments). The connection path must be free of tiles and can’t have diagonal segments.

There are 3 different types of connections:

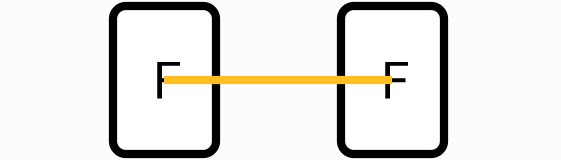
1. One segment

   

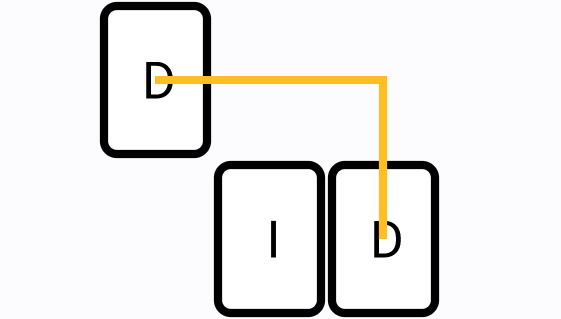
2. Two segments

   

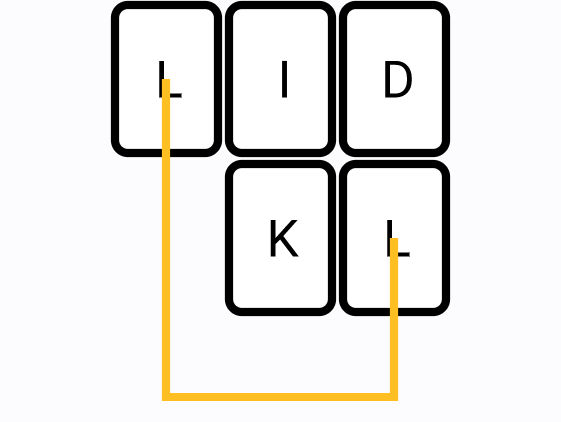
3. Three segments

   

2. Finding a path

There are several ways to find a path between the tiles.

Here’s description of algorithm which FreeShisen app uses:

ALGORITHM TO COMPUTE CONNECTION PATH BETWEEN PIECES A (IA,JA) AND B (IB,JB)
- Delete A and B from the board (consider them as blank spaces)
- Calculate the set H of possible horizontal lines in the board (lines through blank spaces)
- Calculate the set V of possible vertical lines in the board
- Find HA, VA, HB, VB in the sets
- If HA=HB, result is a straight horizontal line A-B
- If VA=VB, result is a straight vertical line A-B
- If HA cuts VB, the result is an L line A-(IA,JB)-B
- If VA cuts HB, the result is an L line A-(IB,JA)-B
- If exists an V line that cuts HA and HB, the result is a Z line A-(IA,JV)-(IB-JV)-B
- If exists an H line that cuts VA and VB, the result is a Z line A-(IV,JA)-(IV,JB)-B

Basically, this is a brute-force search, which is pretty ineffective. It also does not yield the shortest paths.

Another approach is implemented in kshisen:

1. Find a simple path:
   • if tiles are located in the same row or column, the path might be a straight line

2. Find two segments path:

   

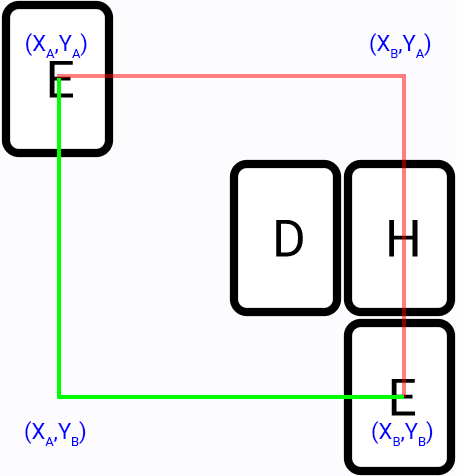
   There are two options for a possible path (red and green lines).

3. Find three segments path:

   From first tile position go in all directions (left, top, right, bottom) and try to find a two segments path to second tile, for example:

   

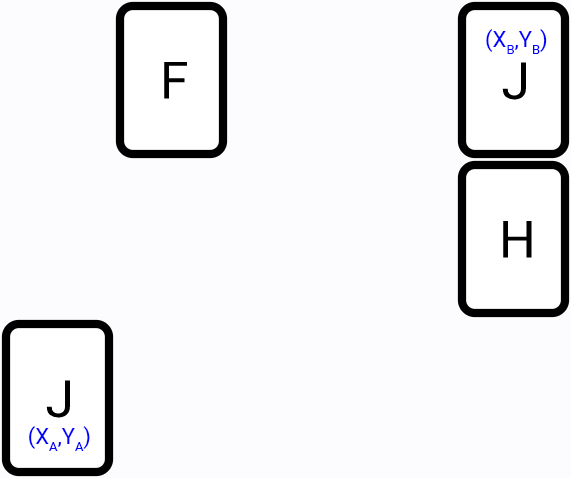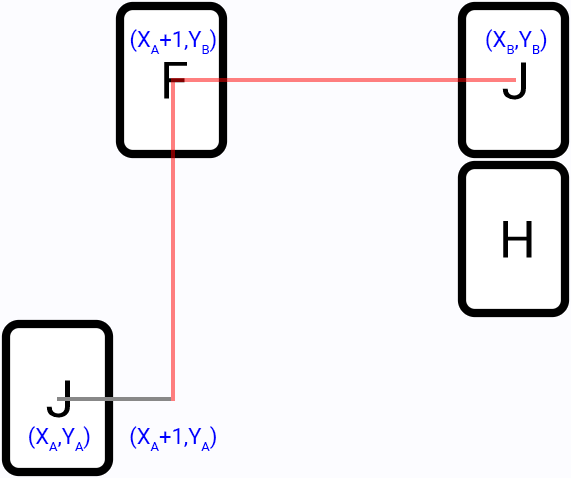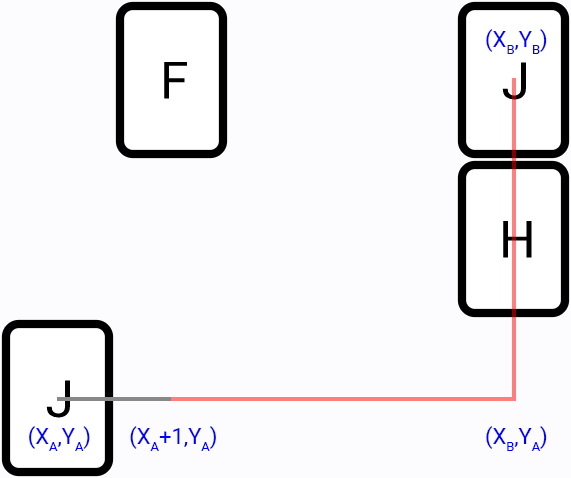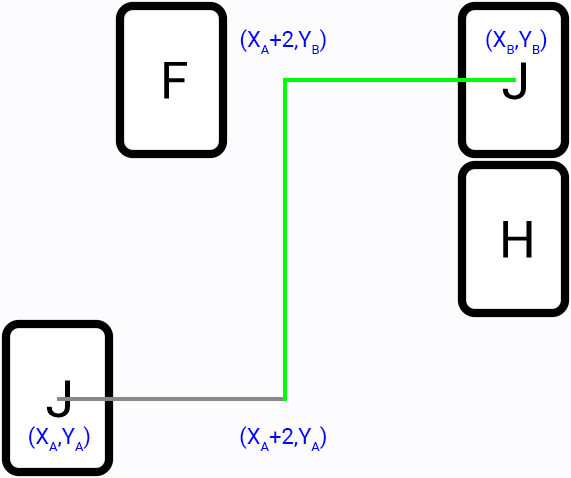
It is the more efficient method, compared to the brute-force, since we perform search only in part of the game field. And most of the time this algorithm will provide the shortest paths.

A note on shortest paths

In some cases the algorithm will produce suboptimal paths.
In a situation where two or more possible paths exist, the solution will depend on in which direction you go first in the 3rd step.

In breadth-first search version we will use a similar technique.

3. Breadth-first search

On each iteration of algorithm expand search in all directions (left, top, right, bottom), keeping track of number of remaining turns.

The outline of an algorithm to find a path from tile A to tile B:

1. Create a queue for storing nodes
2. Expand the start node A, add them to queue
3. If queue:
   • is empty - no path from A to B, exit
   • is not empty - fetch next node N from queue
4. Check N:
   • if N is B, the path is found, exit
   • if N is not B, go to step 3
5. If N is empty cell, expand search from this node
6. Repeat steps 3-6

It is important to understand how we expand nodes. For each node we offset it’s x and y positions in all possible directions and thus make new nodes:

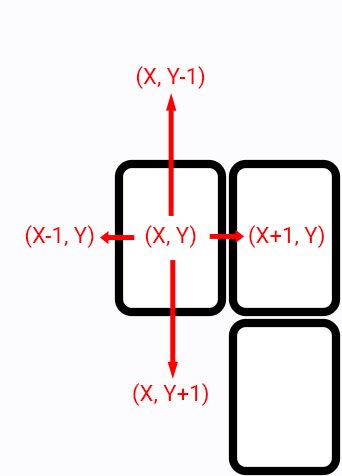
If we expand a node in the same direction as parent node - we don’t change number of remaining turns.

If old and new directions differ, decrease number of turns. If number of remaining turns becomes negative - stop expanding in that direction.

4. Implementation

N.B. I will use Kotlin to implement the algorithm

4.1. Prepare the field

First, create an array of arrays for storing game field, where null is for an empty cell and Char is for a tile:

val width = 6
val height = 4
 // create field and initialize it with nulls
val gameField: Array<Array<Char?>> = Array(width + 2) { Array(height + 2) { null } }

Accessing tile at (x, y) is easy:

val tile: Char? = gameField[x][y]

The width and height are size of the puzzle, and the extra 2’s are needed for building paths for tiles at the edges of the field.

Now, let’s throw some numbers tiles on the field:

val alphabet: MutableList<Char> = ('A'..'Z').toMutableList()
val tiles = ArrayList<Char>(width * height)
val tileCount = 4 // two pairs for each tile
for (i in 0 until (width * height / tileCount)) {
    val tile = alphabet.removeFirst()
    repeat(tileCount) {
        tiles.add(tile)
    }
}
// shuffle tiles
tiles.shuffle()
// fill the field
for (x in 1..width) {
    for (y in 1..height) {
        gameField[x][y] = tiles.removeLast()
    }
}

After these manipulations, our gameField will look like this (. is empty cell):

. . . . . . . .
. B D E F D D .
. B C C B A A .
. A C F F A D .
. E F E E C B .
. . . . . . . .

4.2. Prepare the tools

Create SearchNode class, which will hold information about nodes:

class SearchNode(
    val x: Int, // x position of the node in the field
    val y: Int, // y position of the node in the field
    val turnsLeft: Int, // number of turns left
    val direction: Direction?, // direction of expansion, will be `null` for initial node
    val parent: SearchNode? // parent of this node, for tracking down the path
)

To simplify working with directions, create a separate Direction class with corresponding dx and dy offsets:

enum class Direction(
    val dx: Int,
    val dy: Int
) {
    UP(dx = 0, dy = -1),
    DOWN(dx = 0, dy = 1),
    LEFT(dx = -1, dy = 0),
    RIGHT(dx = 1, dy = 0)
}

Point class will be used to build the resulting path:

class Point(
    val x: Int,
    val y: Int
)

We will need two methods for finding a the path and expanding nodes:

fun findPath(
    ax: Int, ay: Int, // coordinates of the first tile
    bx: Int, by: Int // coordinates of the second tile
): List<Point> {
    TODO("Not implemented")
}

fun expand(node: SearchNode): List<SearchNode> {
    TODO("Not implemented")
}

4.3. Implement the algorithm

Everything is ready for implementing the search algorithm.

For findPath we need to do the following:

1. Check if (ax, ay) and (bx, by) are not the same cell
2. Check if there’re tiles at (ax, ay) and (bx, by) and their labels match
3. Create queue and add initial node to it (tile at (ax, ay))
4. While queue is not empty:
   • remove first node from the queue
   • check if node is the target node - if it is, path found
   • if node is empty, expand it

The code:

fun findPath(
    ax: Int, ay: Int, // coordinates of the first tile
    bx: Int, by: Int // coordinates of the second tile
): List<Point> {
    if (ax == bx && ay == by) {
        // the same cell
        return emptyList()
    }
    val a = gameField[ax][ay]
    val b = gameField[bx][by]
    if (a == null || b == null || a != b) {
        // either one of cells is empty or tile labels does not match, no path
        return emptyList()
    }
    val queue = ArrayDeque<SearchNode>()
    // expand initial node
    val children = expand(
        SearchNode(x = ax, y = ay, turnsLeft = 2, direction = null, parent = null)
    )
    queue.addAll(children)
    while (queue.isNotEmpty()) {
        val node = queue.removeFirst()
        if (gameField[node.x][node.y] != null) {
            // don't need to check tile label, only coordinates
            if (node.x == bx && node.y == by) {
                // path found, trace back to build the list
                val path = ArrayList<Point>()
                var p: SearchNode? = node
                while (p != null) {
                    path.add(Point(p.x, p.y))
                    p = p.parent
                }
                return path
            } else {
                // tile itself cannot be expanded
                // continue to the next iteration
                continue
            }
        }
        // expand node
        queue.addAll(expand(node))
    }
    // there's no path between a and b
    return emptyList()
}

In expand method, for every Direction:

1. Calculate turnsLeft
   • if it’s less than 0, continue to next iteration
2. Calculate newX and newY
   • check if they’re within the bounds of the field (including extra padding)
3. If all checks passed, add new node to candidates list

In code:

fun expand(node: SearchNode): List<SearchNode> {
    val children = ArrayList<SearchNode>()
    for (direction in Direction.values()) {
        val turnsLeft = if (node.direction == null || node.direction == direction) {
            // if the direction is the same (or null, if it's the initial node)
            // keep turnsLeft the same
            node.turnsLeft
        } else {
            // we made a turn
            node.turnsLeft - 1
        }
        if (turnsLeft < 0) {
            // no turns left, try to expand in another direction
            continue
        }
        val newX = node.x + direction.dx
        val newY = node.y + direction.dy
        if (newX !in 0..(width + 1) || newY !in 0..(height + 1)) {
            // make sure we're not getting out of bounds
            continue
        }
        // add node to list
        children.add(SearchNode(newX, newY, turnsLeft, direction, node))
    }
    return children
}

Here is visualization of the algorithm (numbers - turns left, colors - iterations):

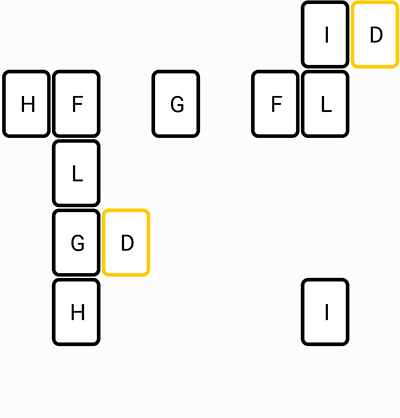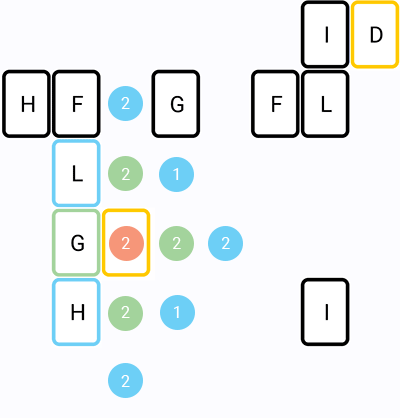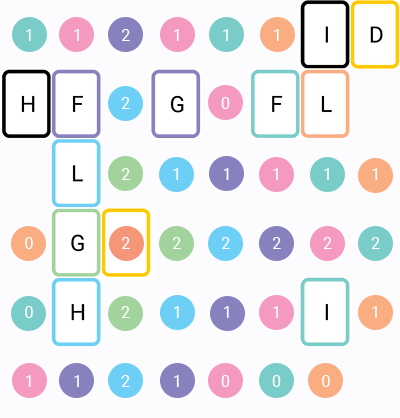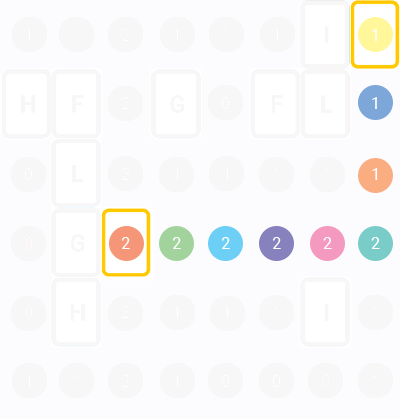
5. Optimizations

As you can see, the algorithm also expands in directions which are guaranteed to fail. We can use some tricks to prune unpromising nodes from the search set.

If tiles are next to each other, no need to run BFS

Manhattan distance is to the rescue:

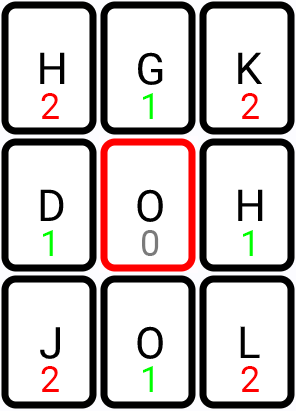
So, we just check if distance is 1:

fun manhattan(x1: Int, y1: Int, x2: Int, y2: Int): Int {
    return abs(x2 - x1) + abs(y2 - y1)
}

fun findPath(...): List<Point> {
    // ...
    if (manhattan(ax, ay, bx, by) == 1) {
        return listOf(Point(ax, ay), Point(bx, by))
    }
    // run bfs
}

This simple check will eliminate startup cost of BFS.

Tiles should have at least one empty cell nearby - otherwise we can’t connect the tiles (unless they are next to each other)

It’s easy to see if one of the tiles is blocked, the path cannot be found:

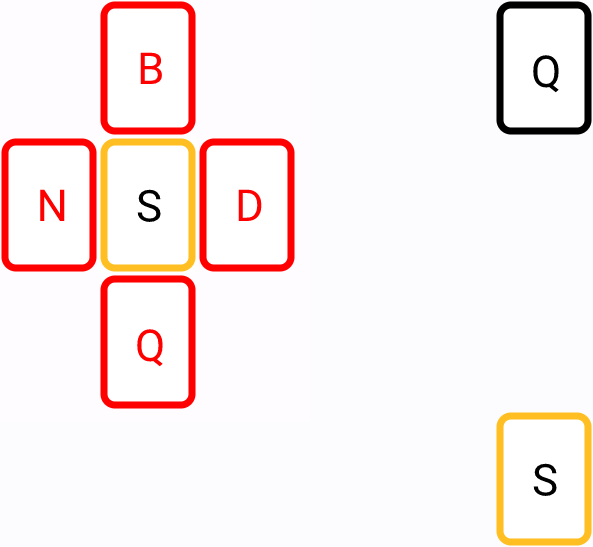
So, let’s add another check to findPath:

fun hasEmptyCells(x: Int, y: Int): Boolean {
    return x - 1 >= 0 && gameField[x - 1][y] == null ||
        x + 1 <= (width + 1) && gameField[x + 1][y] == null ||
        y - 1 >= 0 && gameField[x][y - 1] == null ||
        y + 1 <= (height + 1) && gameField[x][y + 1] == null
}

fun findPath(...): List<Point> {
    // check manhattan distance
    if (!hasEmptyCells(ax, ay) || !hasEmptyCells(bx, by)) {
        return emptyList()
    }
    // run bfs
}

For the last two segments the distance to the second tile must decrease with each step - if it is not, we can stop search in corresponding direction

Here’s another place where manhattan distance comes in handy. Let’s we look closely what happens when we have paths with different number of segments:

1. For a path with one segment, either x or y coordinate is the same - distance always decreases
2. For a path with two segments, x and y coordinates differ, so one segment will close the gap by x axis, and the other will close gap by y axis - distance always decreases
3. For a path with three segments, on the first segment the distance can increase, but then it will decrease (the same as for two segments case)

For example, 3 segments path:

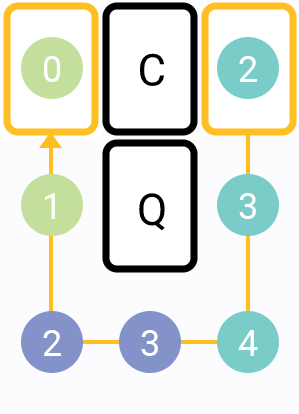
As you can see, the distance raises at the beginning (from 2 to 4), then descreases as we approach target cell on the x and y axes.

So, to improve our algorithm, we add a simple check:

fun expand(node: SearchNode, bx: Int, by: Int): List<SearchNode> {
    // ...
    for (direction in Direction.values()) {
        // ...
        if (turnsLeft < 2) {
            // for the last two segments the distance
            // must decrease on each step in path
            val distance = manhattan(node.x, node.y, bx, by)
            val newDistance = manhattan(newX, newY, bx, by)
            if (distance < newDistance) {
                // try another direction
                continue
            }
        }
        // add node to list
        // ...
    }
    return children
}

6. Final words

Although BFS is not the optimal solution in terms of memory, it always finds the shortest paths and thus works well for shisen-sho.

The code can be found in my repository italankin/shisensho-base:

• Basic game implementation
• Implementation of BFS

And if you haven’t played the game itself, you should definetely try it out. For example, download my Shisen-Sho for Android.

Also, kshisen is a good (and free) one to start, but I personally like Kyodai Mahjongg more.