When 15 puzzle goes wild: a tale of solvability
As a developer of 15 puzzle Android game, I need to generate starting puzzle positions for different puzzle configurations, which must always have a solution - and this, as it turns out, is a challenge.
In this post I will cover so-called solvability of 15 puzzle and different approaches to this topic for various puzzle sizes and types.
1. What is 15 puzzle?
A classic 15 puzzle is a 4x4 grid of numbers from 1 to 15 and one blank square. It looks like this:
The goal of the game is to arrange tiles in order by sliding (vertically or horizontally) tiles:

A tile can be moved only if it stands next to blank (vertically or horizontally, but not diagonally):
Here’s an example of solving 3x3 variant:
2. Generating new positions
It would be a bore to play the game, starting with the same position every time - we need to find a way of generating new ones, preferably unique.
But first, let’s find out how many positions are there.
Because we have 16 squares, and each square can be in 16 states (either one of 15 numbers or blank), the number of possible positions are equal to 16! = 20 922 789 888 000.
However, the only half of them are solvable, so there’s 16! / 2 (roughly 1013) positions, from which we can reach the goal state.
Interesting fact: starting a new 15 puzzle game (at least in my version), you can be certain that no one else in the world has ever seen your position!
So, when generating a puzzle, we must guarantee its solvability - otherwise players won’t be able to reach the goal.
2.1. A set of predefined positions
A solution that comes in mind: take positions which we know are solvable and choose randomly for every new game.
A big drawback of this method is disk space requirement. If we try to store 16! / 2 positions as the array of 16 32-bit integers, it would take at least (16! / 2) * (16 * 4) bytes (~608 TB).
Adding the support for custom sizes, such as 3x3 or 3x4, will require even more space. Of course, the format can be optimized (e.g. instead of 32-bit integers we can use 4-bit and compression), but it will be a large file nonetheless. And we even do not take into the account the time it would take to generate ~1013 positions!
As a workaround, we can take a much smaller set, such as 105. It will make the game simpler in some way, since we exclude a large part of possible positions.
But wait, if we somehow have managed to generate trillions of different positions beforehand, why we can’t do it in runtime?
2.2. Random moves
Rather than preparing a collection of solvable positions, we can generate them on demand.
One method is the following:
- Start with a goal position (
0is a blank square):1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 - Pick a random square, and move
0to that square, for example, number6:1 2 3 4 5 >6< 7 8 9 10 11 12 13 14 15 >0< - By making valid moves, move
0to a target square:1 2 3 4 5 >0< 6 7 9 10 11 8 13 14 15 12 - Repeat steps 2 and 3, until you’re satisfied with the result
This method guarantees that the resulting position will be solvable because we get there by making valid moves. The only question is: how many times do we need to repeat 2-3?
I’ve run a simulation for 4x4, and here’s the chart showing different number of iterations and an average number of moves required to solve the puzzle:
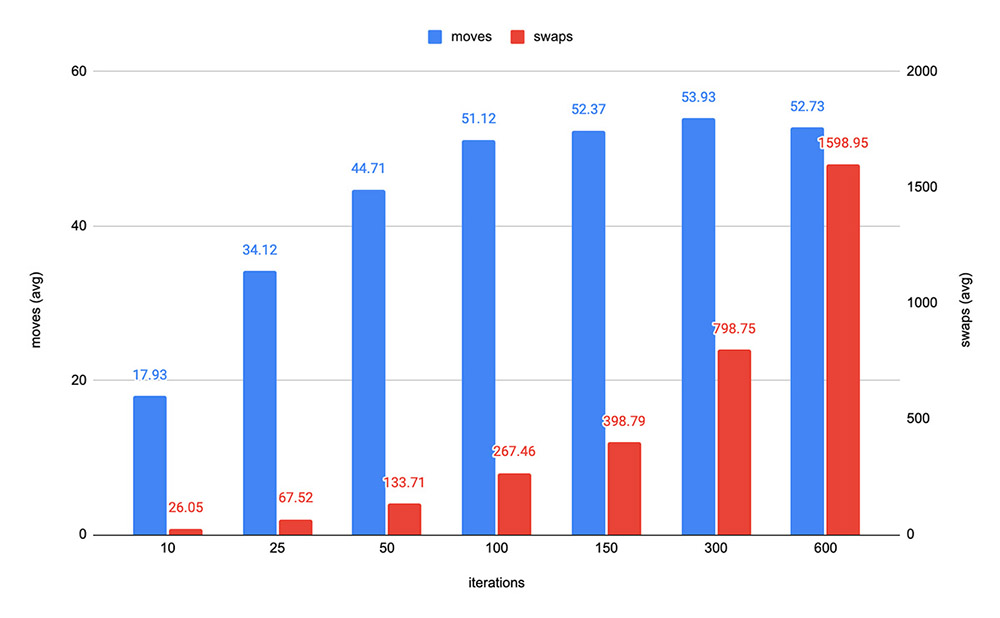
An average solve length is 52.59, so 150 iterations is enough to generate a good puzzle.
But, there’s one issue with this method: number of swaps.
To make a move we swap 0 with another number in the representing array.
Each iteration of the algorithm will require ~2.67 swaps, which is pretty inefficient.
Can we do better?
2.3. Random shuffle with solvability check
Luckily, we can.
The idea is to take goal position and apply a random shuffle. For 4x4, shuffling an array of numbers would require 15 swaps, which is much less than ~398 we saw in the previous section.
How will it perform?
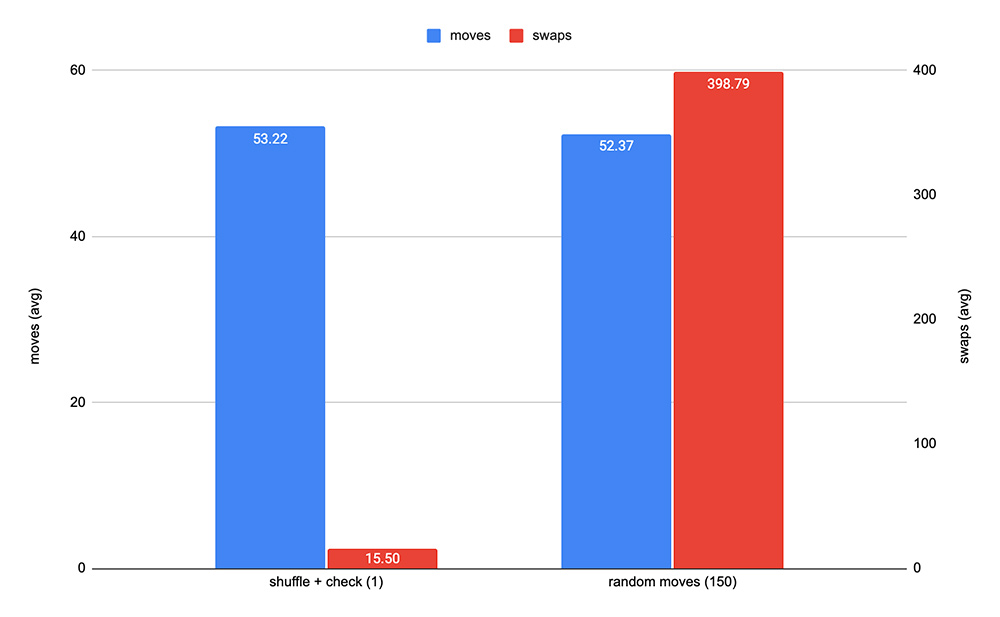
Pretty nice! For 15 swaps (ignore 0.5 part for now) the average result is 53 moves, which is almost one move “harder” than random moves method with 150 iterations.
But, there’s one problem: half of the positions are unsolvable, so 50% of time we’ll put the player in a labyrinth with no way out.
What if there was a way to check whether position is solvable or not? Then we make a shuffle, check, and if the position is not solvable, shuffle again. Because of 50% chance to get solvable configuration, it will require just a few shuffles on average.
But how to check the solvability? There’s an answer to this question too!
3. Solvability
The essence of solvability of an arbitrary position lies in parity (whether a number is even or odd) and inversions.
At first, we need to count number of inversions:
For each number in the starting position (from left to right, from top to bottom) count the numbers which stand after each number and are less than that number (excluding 0)
It is actually total count of numbers that are out of their natural order. For the final position number of inversions is equal to 0 because the numbers are in ascending order.
Let’s look closely how number of inversions change when we make a move. For example, this position has 52 inversions:
8 4 12 3
14 0 9 15
7 2 5 1
10 11 13 6
Calculations
8 4 12 3 14 0 9 15 7 2 5 1 10 11 13 6 → 7
^ 4 12 3 14 0 9 15 7 2 5 1 10 11 13 6 → 3
^ 12 3 14 0 9 15 7 2 5 1 10 11 13 6 → 9
^ 3 14 0 9 15 7 2 5 1 10 11 13 6 → 2
^ 14 0 9 15 7 2 5 1 10 11 13 6 → 9
^ 0 9 15 7 2 5 1 10 11 13 6 → 5
^ 15 7 2 5 1 10 11 13 6 → 8
^ 7 2 5 1 10 11 13 6 → 4
^ 2 5 1 10 11 13 6 → 1
^ 5 1 10 11 13 6 → 1
^ 1 10 11 13 6 → 0
^ 10 11 13 6 → 1
^ 11 13 6 → 1
^ 13 6 → 1
^ 6 → 0
^ ==
52
If we make a move in horizontal direction, number of inversions does not change:
8 4 12 3
14 >9< >0< 15
7 2 5 1
10 11 13 6
Because we do not count 0, the order of other numbers stays the same.
But move in vertical direction changes number of inversions.
If we move 4, it will be 53:
8 >0< 12 3
14 >4< 9 15
7 2 5 1
10 11 13 6
Not only we have changed number of inversions, but the parity is now different: from even (52) to odd (53).
But why does the number of inversions change?
Let’s look at two states of the puzzle, before and after 4 move (we don’t need to look at numbers other than first six because their order preserves):
Before:
8 4 12 3 14 0 - other numbers -
After:
8 0 12 3 14 4 - other numbers -
The move changed number of inversions:
| Number | Numbers less than (before) | Numbers less than (after) | Inversions change |
|---|---|---|---|
8 |
3, 4 |
3, 4 |
0 |
4 |
3 |
- | -1 |
12 |
3 |
3, 4 |
+1 |
3 |
- | - | 0 |
14 |
- | 4 |
+1 |
Total change: +1 (52 → 53)
For puzzles with a width of 4 there will always be 3 numbers between 0 and the moving number.
Because 3 is odd, we’ll never face the situation when count of numbers less than moving number and count of numbers bigger than moving number are equal.
Because of that, possible outcomes are:
- If 3 numbers are bigger than moving number, inversions change by -3
- If 2 of numbers are bigger than moving number, inversions change by -1
- If 1 of numbers is bigger than moving number, inversions change by +1
- If none of numbers are bigger than moving number, inversions change by +3
For puzzles with odd width there are always even count of numbers between, so the parity of inversions is invariant.
Since vertical move flips the parity, 0’s row number in the position shows how many times the parity of inversions has flipped.
Because 0 in the final position is in the last row, we count 0’s position from bottom, starting at 1 (from here forth I’ll count from bottom and starting at 1, unless otherwise noted).
If row number is odd, parity is retained, if it is even, parity is flipped.
Actually, the idea of looking at
0’s position is to find an answer to the question: has the parity changed?
You can also count from 0 and even number will tell you that the parity of inversions hasn’t changed.
So, the position is solvable when:
- The parity of inversions is even and
0in odd row - The parity of inversions is odd and
0in even row
Here’s the full algorithm for checking the solvability:
- Count number of inversions in the position
- If width of the puzzle:
- is odd and number of inversions is even, the puzzle is solvable, otherwise - not solvable
- is even:
- Find the row number of
0, counting from the bottom - If the number of inversions:
- is even and
0’s row number is odd, the puzzle is solvable, otherwise - not solvable - is odd and
0’s row number is even, the puzzle is solvable, otherwise - not solvable
- is even and
- Find the row number of
Example: for the starting position:
12 13 11 2
4 5 3 14
1 9 15 6
8 7 0 10
- Count number of inversions: 52
- Width of the puzzle is even (4), so find the
0’s row number: 1 - Number of inversions (52) is even, and
0’s row number (1) is odd, so the puzzle is solvable (in fact, in 57 moves)
What to do if the puzzle is unsolvable?
As I said earlier, we could just shuffle the array until we get a solvable one. But, actually, we can make use of one little trick:
Swapping two largest numbers (e.g. for 4x4 it’s
14and15) will flip the parity of number of inversions
That is, if we get an unsolvable configuration, just by exchanging two numbers we make the puzzle solvable.
This is where that 0.5 came from: 50% of time we get solvable configuration right away (in 15 swaps), and for other 50% situations we make an additional swap of two largest numbers (16th swap), averaging total number of swaps to 15.5.
4. Extending the puzzle
4.1. Non-square configurations
Maybe you have noted that solvability of a position is tied to width of a puzzle, but there’s nothing about height. There’s no mistake: height can be any number larger than 1, and we only look at the width. So, the rules are the same as for square variations.
4.2. Snake, spiral and others
Until this moment we only considered variants where numbers in the final position come in ascending order, from left to right, from top to bottom.
But, we can think of puzzles where rules are different, for example, the “snake”:
1 2 3 4
8 7 6 5
9 10 11 12
0 15 14 13
Unfortunately, our algorithm will not work for this configuration, and we need to come up with a new one.
Let’s look at how we count number of inversions:
For every number in the starting position (from left to right, from top to bottom)
Note that we traverse position in the order numbers appear in the final position (o is start, x is end):
o → → →
→ → → →
→ → → →
→ → → x
But for ‘snake’ it is different:
o → → ↘
↙ ← ← ↙
↘ → → ↘
x ← ← ↙
We just need to reverse the direction of iteration for every other row. And, actually, we don’t need to bother about width of a puzzle.
A side note on width
To understand why we don't check the width of the puzzle, let's see what happens when we make a move in snake:1 2 3 4 8 7 6 5 >9< 10 11 12 >0< 15 14 13To simplify, we leave only the numbers that are affected by the move:- - - - - - - - >0< 10 11 12 >9< 15 14 13In any case there will be even count of numbers between, and this is also true for odd width variations:1 2 3 6 >0< 4 7 >5< 8- - - 6 >5< - 7 >0< -Which means the parity of inversions is invariant.
The algorithm is simple:
- Traverse the position in the order of numbers appear on the goal position and count number of inversions
- If number of inversions is even, the puzzle is solvable, otherwise - not solvable
And, for “spiral”:
o → → ↘
↗ → ↘ ↓
↑ x ↙ ↓
↖ ← ← ↙
The algorithm is exactly the same.
And it will work for any other configuration where you can draw a line with a pen by following number order without making gaps, e.g.:
↗ ↘ x o
↑ ↓ ↑ ↓
↑ ↘ ↗ ↓
↖ ← ← ↙
4.3. Random missing number
There’s another interesting configuration worth noting: rather than removing 16 in 4x4 puzzle, remove any other number.
If you try to apply the classic algorithm on such configurations, you will find that 50% of the puzzles will be unsolvable, although algorithm states the opposite. Let’s see:
12 8 7 15
0 6 4 1
10 9 13 11
3 16 14 5
In this position the number 2 is missing, it has 50 inversions and 0’s row number is 3 - so, it must be solvable.
But, if you try to solve the puzzle, you will end up with something like this (10 and 11 are in wrong order):
1 0 3 4
5 6 7 8
9 11<>10 12
13 14 15 16
If you dig a little deeper, you will find the classic algorithm is not working only for positions where 0’s row number in the goal position is even.
What can be done here?
5. Universal algorithm
We need to pay attention to two things:
- Parity of number of inversions in the start and goal positions
- Parity of
0’s row number in the start and goal positions
For puzzles with odd width we check whenever number of inversions in the start and goal positions have the same parity.
For even width, as we found earlier, we need to find how many times the parity of inversions has flipped.
Because the 0 in the goal position now can be on any row, instead of counting row from the bottom, we take the difference between row positions in the start and goal.
In general, the algorithm for reachability from start position S to goal position G is:
- Calculate number of inversions in
G-I(G) - Calculate number of inversions in
S-I(S) - If:
- width is odd and
I(G)andI(S)have the same parity,Gis reachable fromS(in other words,Sis solvable) - width is even:
- Find the row number1 where blank is located in
G-B(G) - Find the row number where blank is located in
S-B(S) - If
I(G)- is even and
I(S)andB(G) - B(S)2 have the same parity,Gis reachable fromS - is odd and
I(S)andB(G) - B(S)have different parity,Gis reachable fromS
- is even and
- Find the row number1 where blank is located in
- width is odd and
- In other cases
Gis unreachable fromS.
1 You can count from top or bottom, from 0 or 1, it doesn’t matter. Because in the next step we subtract row numbers, we just want the relative positions of blank in the start and goal states
2 B(G) - B(S) can be replaced with B(G) + B(S), because we’re only interested in parity
A side note
Actually, you don't need a special algorithm to generate a valid puzzle of arbitrary configuration.
You just create a mapping of your goal position to the classic goal position and perform actions on the backing classic field, but display your mapped position instead.
Here’s whole the algorithm written in Java:
/**
* Calculate number of inversions in the {@code list}
*/
int inversions(
List<Integer> list
) {
int inversions = 0;
int size = list.size();
for (int i = 0; i < size; i++) {
int n = list.get(i);
if (n <= 1) {
// no need to check for 0 and 1
continue;
}
for (int j = i + 1; j < size; j++) {
int m = list.get(j);
if (m > 0 && n > m) {
inversions++;
}
}
}
return inversions;
}
/**
* Check whether {@code goal} is reachable from {@code start}
* for a puzzle with {@code width}
*/
boolean isSolvable(
List<Integer> start,
List<Integer> goal,
int width
) {
int startInversions = inversions(start);
int goalInversions = inversions(goal);
if (width % 2 == 0) {
int goalZeroRow = goal.indexOf(0) / width;
int startZeroRow = start.indexOf(0) / width;
if (goalInversions % 2 == 0) {
return startInversions % 2 == (goalZeroRow + startZeroRow) % 2;
} else {
return startInversions % 2 != (goalZeroRow + startZeroRow) % 2;
}
// the above if-else statement can be replaced with:
// return (goalInversions + startInversions + goalZeroRow + startZeroRow) % 2 == 0;
} else {
// 'startInversions' should have the same parity as 'goalInversions'
return startInversions % 2 == goalInversions % 2;
}
}
6. Bonus: random goals
A free lunch: the universal algorithm works for any goal configuration, regardless of zero position or missing number.
7. Final words
If you made this far, congratulations! Now you know (I hope) a little more of this (seemingly) simple game of 15 puzzle.
The source code of my game is hosted on GitHub. There are also tests you can play with, trying different game types and configurations.
And, in case you want to play the game itself, you can download it from Google Play.